Ecuaciones exponenciales
Los mejores cursos GRATIS
Ver TODOS los 1707 cursos GRATIS
Participa en el Foro y los Chats

Inicio » Cursos » Secundaria ESO » Matemáticas Secundaria ESO » Ecuaciones » Ecuación exponencial
Curso gratis de Ecuaciones
(20h)
- http://www.aulafacil.com/cursos/l29545/secundaria-...">

Compartir
en Facebook - http://www.aulafacil.com/cursos/l29545/secundaria-...">

Compartir
en Twitter - http://www.aulafacil.com/cursos/l29545/secundaria-...">

Enviar
amigo - http://www.aulafacil.com/cursos/l29545/secundaria-...">

Reportar
Error - http://www.aulafacil.com/cursos/l29545/secundaria-...">

Imprimir
artículo
Lección 23 Índice
Ecuación exponencial

Oir Lecc.
La ecuación exponencial entra dentro del grupo de ecuaciones no polinómicas. En ella la incógnita aparece en el exponente.
Veamos algunos ejemplos:
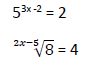
Para resolver las ecuaciones exponenciales hay diversos métodos:
a) Operar con la ecuación para conseguir que los dos miembros de la ecuación tengan la misma base.
Si:
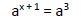
Al tener la misma base igualamos los exponentes:
x + 1 = 3
b) Aplicar logaritmos:
Aplicamos logaritmos de la misma base a ambos miembros de la ecuación:
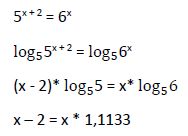
Y ya podemos resolver como una ecuación polinómica.
c) Cambio de incógnita: este método se suele utilizar cuando la ecuación es más compleja.
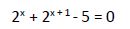
Hacemos un cambio de variable:
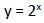
Por lo que:
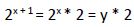
La ecuación quedaría:
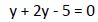
Y la resolveríamos como una ecuación polinómica. Una vez calculada la raíz “y” de esta ecuación, calcularíamos “x” aplicando su relación de equivalencia.
En todo caso, cuando el alumno se enfrenta a la resolución de una ecuación exponencial a veces debe operar previamente, transformando la ecuación, simplificándola, antes de poder aplicar alguno de los métodos anteriores.
Veamos diversos ejemplos:
a) Ejemplos de ecuaciones resueltas aplicando el método de igualar las bases y/o el método de aplicar logaritmos.
1er ejemplo
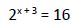
1.1. Igualando las bases:
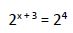
Al tener la misma base igualamos los exponentes:
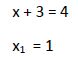
Comprobamos en la ecuación original si esta solución satisface la igualdad:
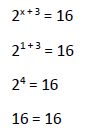
Por lo tanto la solución hallada (x1 = 1) es solución de la ecuación inicial.
1.2. Aplicando logaritmos:
Aplicamos logaritmos de la misma base a ambos miembros de la ecuación.
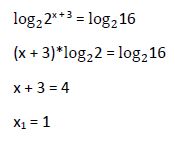
2º ejemplo
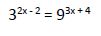
2.1. Igualando las bases:
Operamos tratando de buscar que tengan la misma base en ambos miembros:
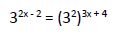
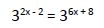
Al tener la misma base igualamos los exponentes:
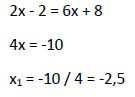
Comprobamos en la ecuación original si esta solución satisface la igualdad:
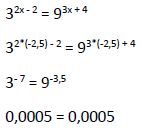
Por lo tanto la solución hallada (x1 = -2,5) es solución de la ecuación inicial.
2.2. Aplicando logaritmos:
Aplicamos logaritmos de la misma base a ambos miembros de la ecuación.
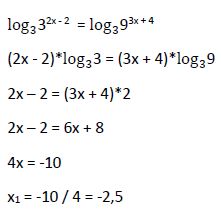
3er ejemplo
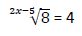
Luego:
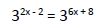
Al tener la misma base igualamos los exponentes:
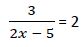
Y seguimos operando:
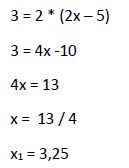
Comprobamos en la ecuación original si esta solución satisface la igualdad:
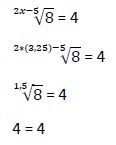
Por lo tanto la solución hallada (x1 = 3,25) es solución de la ecuación inicial.
4º ejemplo
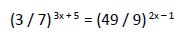
4.1. Igualando las bases:
En primer lugar vamos a operar con la ecuación para tratar de tener la misma base en ambos miembros.
Si nos fijamos en el miembro de la derecha podemos ver:

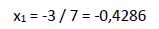
Comprobamos en la ecuación original si esta solución satisface la igualdad:
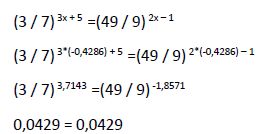
Por lo tanto la solución hallada (x1 = -0,4286) es solución de la ecuación inicial.
5º ejemplo
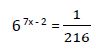
5.1. Igualando las bases:
En primer lugar vamos a operar con la ecuación para tratar de tener la misma base en ambos miembros.
Si nos fijamos en el miembro de la derecha podemos ver:
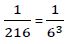
Aplicando una propiedad de la potencia tenemos:
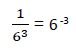
Sustituyendo en la ecuación inicial:
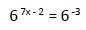
Con esta transformación hemos conseguido tener la misma base en ambos miembros de la ecuación, por lo que podemos igualar los exponentes:
7x - 2 = -3
7x = -1
x1 = -1 / 7 = -0,1429
Comprobamos en la ecuación original si esta solución satisface la igualdad:
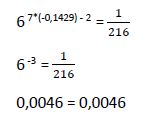
Por lo tanto la solución hallada (x1 = -0,1429) es solución de la ecuación inicial.
6º ejemplo
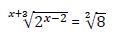
6.1. Igualando las bases:
Luego:
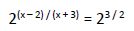
Al tener la misma base igualamos los exponentes:
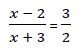
Y seguimos operando:
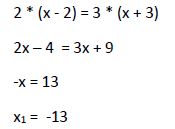
Comprobamos en la ecuación original si esta solución satisface la igualdad:
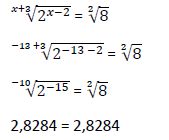
Por lo tanto la solución hallada (x1 = -13) es solución de la ecuación inicial.
7º ejemplo
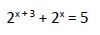
7.1. Aplicando logaritmos:
Luego:
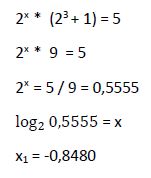
De dónde sale el 1 y por qué .

